Question: 11 -
A man completes a journey in 5 hours. He completes the first half of the journey at a speed of 20 km/hr and the second half at a speed of 25 km/hr. What is the total journey in km?
-
5.4 km
-
6.4 km
-
4.4 km
-
3.4 km
Answer:
5.4 km
Solution:
Let the time taken to complete the first half of the journey = X hour
∴ the time taken to complete the second half of the journey = (5 - X)
Distance covered in first half = Distance covered in second half
Distance covered in first half = speed * time→20*X=20X
Distance covered in second half = speed * time→25 * (5-X)
So, 20X = 25 * (5-X)
20X = 125 -25X
45X = 125
X= 125⁄45= 2.7 km
X is the distance covered in first half which is equal to the distance covered in the second half.
So to get the total journey we will multiply X with 2.
Total journey in Km = 2.7 x 2 = 5.4 km
Let the time taken to complete the first half of the journey = X hour
∴ the time taken to complete the second half of the journey = (5 - X)
Distance covered in first half = Distance covered in second half
Distance covered in first half = speed * time→20*X=20X
Distance covered in second half = speed * time→25 * (5-X)
So, 20X = 25 * (5-X)
20X = 125 -25X
45X = 125
X= 125⁄45= 2.7 km
X is the distance covered in first half which is equal to the distance covered in the second half.
So to get the total journey we will multiply X with 2.
Total journey in Km = 2.7 x 2 = 5.4 km
Question: 12 -
If a man runs at 24 km/hr instead of 20 km/hr he could run 40 km more. Find the actual distance travelled by him.
-
100 km
-
250 km
-
150 km
-
200 km
Answer:
200 km
Solution:
Let the actual distance travelled by man = X km
In this problem, time is same for both the situations when the man runs at 20 km/hr and 24 km/hr.
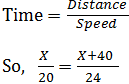
24X = 20X + 800
4X = 800
X =800⁄4= 200 km
Let the actual distance travelled by man = X km
In this problem, time is same for both the situations when the man runs at 20 km/hr and 24 km/hr.
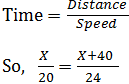
24X = 20X + 800
4X = 800
X =800⁄4= 200 km
Question: 13 -
A bus travels 50% faster than a car. Both start moving at the same time from station P and reach station Q at the same time. The stations are 100 km apart. If on the way the bus stops at the bus stop for 10 minutes, find the speed of the car.
-
300 km/hr
-
315 km/hr
-
410 km/hr
-
415 km/hr
Answer:
300 km/hr
Solution:
Let the speed of the car = X km/hr
∴ the speed of the bus will be = X *150⁄100=3⁄2X
Both bus and car take equal time to reach the station Q.
The bus stops for 10 minutes at the bus stop. So if the bus would not have stopped it would have reached the station Q, 10 minutes earlier and the difference between the time taken by the car and bus would have been = 10 minutes or10⁄60 hours.
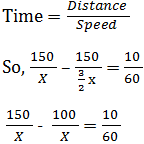
3000 = 10 X
X =3000⁄10= 300 km/hr
Let the speed of the car = X km/hr
∴ the speed of the bus will be = X *150⁄100=3⁄2X
Both bus and car take equal time to reach the station Q.
The bus stops for 10 minutes at the bus stop. So if the bus would not have stopped it would have reached the station Q, 10 minutes earlier and the difference between the time taken by the car and bus would have been = 10 minutes or10⁄60 hours.
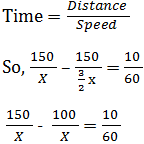
3000 = 10 X
X =3000⁄10= 300 km/hr
Question: 14 -
Two buses 200 km apart, start moving from the bus stations at the same time towards each other on parallel roads. If they cross each other at a distance of 120 km from one of the bus stations, find the ratio of their speeds.
-
5⁄2
-
6⁄2
-
4⁄2
-
3⁄2
Answer:
3⁄2
Solution:
The total distance between the bus stations is 200 km. So, when the buses cross each other the sum of the distances travelled the buses will be equal to 200 km.
We have given that buses cross each other at a distance of 120 km from one of the stations. So one bus covers a distance of 120 km and the other bus covers the rest of the distance (200-120=80km).
The ratio of their speeds will be equal to the ratio of distances covered by them.
So, ratio of speeds = 120⁄80→3⁄2
The total distance between the bus stations is 200 km. So, when the buses cross each other the sum of the distances travelled the buses will be equal to 200 km.
We have given that buses cross each other at a distance of 120 km from one of the stations. So one bus covers a distance of 120 km and the other bus covers the rest of the distance (200-120=80km).
The ratio of their speeds will be equal to the ratio of distances covered by them.
So, ratio of speeds = 120⁄80→3⁄2
Question: 15 -
Including stoppages the speed of a bus is 60 km/hr and excluding stoppages its speed is 65 km/hr. For how long the bus stops in an hour?
-
3 minutes
-
7 minutes
-
6 minutes
-
4 minutes
Answer:
4 minutes
Solution:
The bus covers a distance of 60 km in an hour if it stops at the bus stops.
The bus covers a distance of 65 km in an hour if it does not stop at the bus stops.
Due to stoppages it covers 5 km less.
If it does not stop it will cover 5 km more.
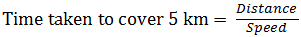
Time =5⁄65→1⁄15hour
We need answer in minutes so 1⁄15* 60=4 minutes
The bus covers a distance of 60 km in an hour if it stops at the bus stops.
The bus covers a distance of 65 km in an hour if it does not stop at the bus stops.
Due to stoppages it covers 5 km less.
If it does not stop it will cover 5 km more.
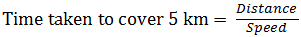
Time =5⁄65→1⁄15hour
We need answer in minutes so 1⁄15* 60=4 minutes