Question: 31 -
A man swims 12 km downstream and 10 km upstream. If he takes 2 hours each time, what is the speed of the stream?
-
0.7 km/hr
-
1 km/hr
-
0.5 km/hr
-
1.5 km/hr
Answer:
0.5 km/hr
Solution:
Speed downstream = 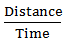 =
= 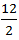 = 6 km/hr
= 6 km/hr
Speed downstream = 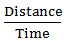 =
= 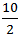 = 5 km/hr
= 5 km/hr
Apply formula: Speed of stream = 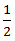 (speed downstream - speed upstream)
(speed downstream - speed upstream)
X = 6 km/hr
Y= 5 km/hr
∴ Required speed = 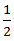 (6 -5) km/hr
(6 -5) km/hr
= 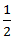 ∗ 1= 0.5 km/hr
∗ 1= 0.5 km/hr
Speed downstream = 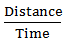 =
= 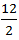 = 6 km/hr
= 6 km/hr
Speed downstream = 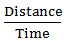 =
= 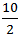 = 5 km/hr
= 5 km/hr
Apply formula: Speed of stream = 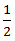 (speed downstream - speed upstream)
(speed downstream - speed upstream)
X = 6 km/hr
Y= 5 km/hr
∴ Required speed = 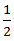 (6 -5) km/hr
(6 -5) km/hr
= 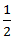 ∗ 1= 0.5 km/hr
∗ 1= 0.5 km/hr
Question: 32 -
A man can row a boat at a speed of 20 km/hr in still water. If the speed of the stream is 5 km/hr, in what time he can row a distance of 75 km downstream?
-
1.5 hours
-
2.5 hours
-
2 hours
-
3 hours
Answer:
3 hours
Solution:
Speed of boat = 20 km/hr
Speed of stream = 5 km/hr
∴ Speed downstream = 20 + 5= 25 km/hr
Required Time = 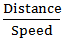 =
= 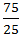 = 3 hours
= 3 hours
Speed of boat = 20 km/hr
Speed of stream = 5 km/hr
∴ Speed downstream = 20 + 5= 25 km/hr
Required Time = 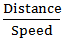 =
= 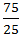 = 3 hours
= 3 hours
Question: 33 -
A boatman can row a certain distance down the stream in 2 hours and can row the same distance up the stream in 3 hours. If the velocity of the stream is 4km/hr, what is the speed of the boat in still water?
-
12km/hr
-
8km/hr
-
40km/hr
-
20km/hr
Answer:
20km/hr
Solution:
Let the distance = x km
Time is taken in downstream = 2 hour
So, the speed of downstream is x/2 km/hr
Similarly, the time is taken in upstream = 3 hr
So, the speed of upstream is x/3 km/hr
Speed of stream = 4 km/hr
Now, apply the formula.
Speed of stream = (1/2) [speed of downstream - speed of upstream] Or, 4 = (1/2) [x/2 - x/3]
Take LCM of 2 and 3 = 6
Now, (½) [(3x-2x)/6] = 4
Or, x= 48 km
Now, speed of downstream = 48/2 = 24 km/hr
And the speed of upstream = 48/3 = 16km/hr
Now, apply the formula.
Speed of boat in still water = (½) [24+16] = 20km/hr
Let the distance = x km
Time is taken in downstream = 2 hour
So, the speed of downstream is x/2 km/hr
Similarly, the time is taken in upstream = 3 hr
So, the speed of upstream is x/3 km/hr
Speed of stream = 4 km/hr
Now, apply the formula.
Speed of stream = (1/2) [speed of downstream - speed of upstream] Or, 4 = (1/2) [x/2 - x/3]
Take LCM of 2 and 3 = 6
Now, (½) [(3x-2x)/6] = 4
Or, x= 48 km
Now, speed of downstream = 48/2 = 24 km/hr
And the speed of upstream = 48/3 = 16km/hr
Now, apply the formula.
Speed of boat in still water = (½) [24+16] = 20km/hr
Question: 34 -
A boat covers 800 meters in 600 seconds against the stream and returns downstream in 5 minutes. What is the speed of the boat in still water?
-
1 m/s
-
2 m/s
-
2.5 m/s
-
1.5 m/s
Answer:
2 m/s
Solution:
Speed upstream = 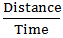 =
= 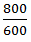 =
= 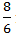 m/s
m/s
Speed downstream = 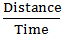 =
= 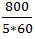 =
= 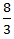 m/s
m/s
Apply formula: Speed in still water = 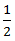 (speed downstream + speed upstream)
(speed downstream + speed upstream)
X = 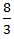 m/s
m/s
Y = 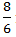 m/s
m/s
∴ Speed in still water = 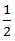
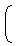
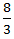 +
+ 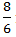

= 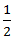 ∗ 4 = 2 m/s
∗ 4 = 2 m/s
Speed upstream = 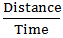 =
= 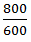 =
= 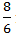 m/s
m/s
Speed downstream = 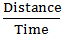 =
= 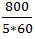 =
= 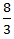 m/s
m/s
Apply formula: Speed in still water = 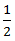 (speed downstream + speed upstream)
(speed downstream + speed upstream)
X = 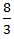 m/s
m/s
Y = 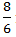 m/s
m/s
∴ Speed in still water = 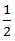
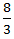 +
+ 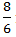

= 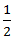 ∗ 4 = 2 m/s
∗ 4 = 2 m/s
Question: 35 -
A man can row 9[1/3] km/hr in still water. He finds that it takes thrice as much time to row upstream as to row downstream (same distance). Find the speed of the current.
-
4[2/3] km/hr
-
3[1/9] km/hr
-
1[1/4] km/hr
-
3[1/3] km/hr
Answer:
4[2/3] km/hr
Solution:
The speed of man in still water is 9[1/3]
ATQ, time taken while rowing upstream = 3k
Time taken while rowing downstream = k
We know that time is inversely proportional to speed.
Upstream speed (y) = k
Downstream (x) = 3k
Now, apply the formula.
Speed of man in still water = (1/2) [speed of downstream + speed of upstream]
Or, 9[1/3] = (1/2) [3k+ k]
Or, 28/3 = 2k
Or, k = 14/3
So, upstream speed (y) = 14/3
And, downstream speed (x) = (14/3) * 3 = 14
Now, apply the formula.
Speed of current = (1/2) [downstream speed - upstream speed]
= (½) [14 - 14/3]
= 28/6 = 4[2/3]
The speed of man in still water is 9[1/3]
ATQ, time taken while rowing upstream = 3k
Time taken while rowing downstream = k
We know that time is inversely proportional to speed.
Upstream speed (y) = k
Downstream (x) = 3k
Now, apply the formula.
Speed of man in still water = (1/2) [speed of downstream + speed of upstream]
Or, 9[1/3] = (1/2) [3k+ k]
Or, 28/3 = 2k
Or, k = 14/3
So, upstream speed (y) = 14/3
And, downstream speed (x) = (14/3) * 3 = 14
Now, apply the formula.
Speed of current = (1/2) [downstream speed - upstream speed]
= (½) [14 - 14/3]
= 28/6 = 4[2/3]