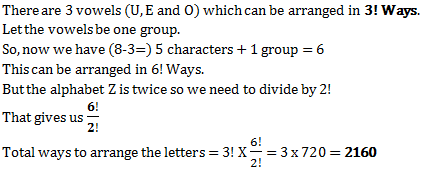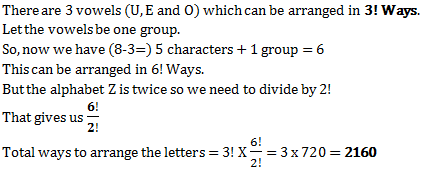Question: 11 -
There are 20 points in a plane, how many triangles can be formed by these points if 5 are colinear?
-
1129
-
1130
-
550
-
1140
Answer:
1130
Solution:
Number of points in plane n = 20.
Number of colinear points m = 5.
Number of triangles from by joining n points of which m are colinear = nC3 – mC3
Therefore the number of triangles = 20C3 – 5C3 = 1140-10 = 1130.
Number of points in plane n = 20.
Number of colinear points m = 5.
Number of triangles from by joining n points of which m are colinear = nC3 – mC3
Therefore the number of triangles = 20C3 – 5C3 = 1140-10 = 1130.
Question: 12 -
There are 30 people in a group. If all shake hands with one another , how many handshakes are possible?
-
29! + 1
-
30!
-
870
-
435
Answer:
435
Solution:


Question: 13 -
In how many ways can we select 6 people out of 10, of which a particular person is not included?
-
10C3
-
9C6
-
9C5
-
9C4
Answer:
9C6
Solution:
One particular person is not included we have to select 6 persons out of 9 which can be done in 9C6 ways.
One particular person is not included we have to select 6 persons out of 9 which can be done in 9C6 ways.
Question: 14 -
Find the number of rectangles and squares in an 8 by 8 chess board respectively.
-
1092, 204
-
296, 204
-
204, 1092
-
204, 1296
Answer:
1092, 204
Solution:
Chess board consists of 9 horizontal 9 vertical lines. A rectangle can be formed by any two horizontal and two vertical lines. Number of rectangles = 9C2 × 9C2 = 1296. For squares there is one 8 by 8 square four 7 by 7 squares, nine 6 by 6 squares and like this
Number of squares on chess board = 12+22…..82 = 204
Only rectangles = 1296-204 = 1092.
Chess board consists of 9 horizontal 9 vertical lines. A rectangle can be formed by any two horizontal and two vertical lines. Number of rectangles = 9C2 × 9C2 = 1296. For squares there is one 8 by 8 square four 7 by 7 squares, nine 6 by 6 squares and like this
Number of squares on chess board = 12+22…..82 = 204
Only rectangles = 1296-204 = 1092.
Question: 15 -
In how many ways can we arrange the word ‘FUZZTONE’ so that all the vowels come together?
-
6
-
1440
-
4320
-
2160
Answer:
2160
Solution: