Engineering Quantitative Aptitude English Reasoning General Knowledge Coding Others

Quiz: Permutations and Combinations

To View Tricks: Login Required

Number of Questions: 40

Question: 36 -

How many words, with or without meaning, can be formed using all letters of the word EQUATION using each letter exactly once?

Options:

  1. 38,400

  2. 40,320

  3. 38,320

  4. 39,320

    5. Answer:

    40,320
    Solution:

    The Word EQUATION has exactly 8 letters which are all different.
    Therefore the number of words that can be formed = Number of permutations of 8 letters taken all at a time.
    = P (8, 8) = 8!
    = 8 × 7 x 6 × 5 x 4 x 3 x 2 × 1
    = 40,320

Question: 37 -

Ten participants are participating in a competition. In how many ways can the first three prizes be won?

Options:

  1. 920

  2. 720

  3. 680

  4. 820

    5. Answer:

    720
    Solution:

    Out of 10 participants, the first three prizes can be won in,
    10P3 = 10! / (10 - 3)!
    = 10 x 9 x 8
    = 720 ways

Question: 38 -

A box contains 2 red balls, 3 black balls, and 4 white balls. Find the number of ways by which 3 balls can be drawn from the box in which at least 1 black ball should be present.

Options:

  1. 32

  2. 48

  3. 64

  4. 96

    5. Answer:

    64
    Solution:

    The possible combination could be (1 black ball and 2 non-black balls), (2 black balls and 1 non- black ball), and (only 3 black balls).

    Therefore the required number of combinations = (3C1 * 6C2) + (3C2 * 6C1) + (3C3)
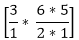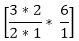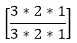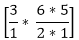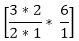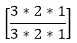    r,Apti Permutation and Combination + Apti Permutation and Combination + Apti Permutation and Combination = 45+18+1 = 64

Question: 39 -

In how many ways can a cricketer can score 200 runs with fours and sixes only?

Options:

  1. 16

  2. 19

  3. 17

  4. 13

    5. Answer:

    17
    Solution:

    200 runs can be scored by scoring only fours or through a combination of fours and sixes.
    Possibilities are 50 x 4, 47 x 4 + 2 x 6, 44 x 4 + 4 x 6 ... A total of 17 ways

Question: 40 -

Seven different objects must be divided among three people. In how many ways can this be done if one or two of them must get no objects? 

Options:

  1. 180

  2. 36

  3. 381

  4. 84

    5. Answer:

    381
    Solution:

    Let the three people be A, B, and C.

    If 1 person gets no objects, the 7 objects must be distributed such that each of the other two get 1 object at least.
    This can be done as 6 & 1, 5 & 2, 4 & 3 and their rearrangements.
    The answer would be ( 7C6 + 7C5 + 7C4 ) x 3! = 378
    Also, two people getting no objects can be done in 3 ways.
    Thus, the answer is 378 + 3 = 381