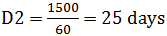Question: 6 -
A cistern can be filled by an inlet in 6 hours and can be emptied by an outlet in 8 hours. If the inlet and outlet are opened together, in what time the cistern can be filled?
-
26 hours
-
20 hours
-
24 hours
-
18 hours
Answer:
24 hours
Solution:
Part of the tank filled by the inlet in one hour = 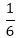
Part of the tank emptied by the outlet in one hour = 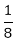
Net part of the tank filled in one hour = 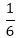 -
- 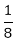
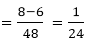
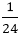 part of the tank is filled in one hour
part of the tank is filled in one hour
∴ The whole tank will be filled in 24 hours.
Solution 2:
Apply formula; =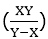
X = 6 hours
Y = 8 hours
∴ Required time = 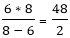 = 24 hours
= 24 hours
Part of the tank filled by the inlet in one hour = 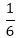
Part of the tank emptied by the outlet in one hour = 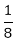
Net part of the tank filled in one hour = 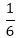 -
- 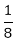
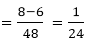
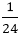 part of the tank is filled in one hour
part of the tank is filled in one hour
∴ The whole tank will be filled in 24 hours.
Solution 2:
Apply formula; =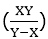
X = 6 hours
Y = 8 hours
∴ Required time = 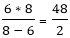 = 24 hours
= 24 hours
Question: 7 -
Pipe A can fill a tank in 12 minutes whereas pipe A along with pipe B can fill the same tank in 8 minutes. In what time pipe B alone can fill the tank?
-
25
-
24
-
22
-
20
Answer:
24
Solution:
Part of the tank filled by pipe A in one minute=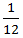
Part of the tank filled by A+B in one minute =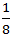
Part of the tank filled by B alone =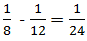
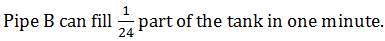
∴ Pipe B will fill the whole tank in 24 minutes.
Solution 2:
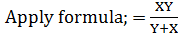
X= 12 minutes
Y=?
As per question;
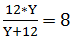
12Y= 8Y+96
4Y= 96
Y = 24 minutes
Part of the tank filled by pipe A in one minute=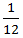
Part of the tank filled by A+B in one minute =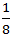
Part of the tank filled by B alone =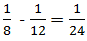
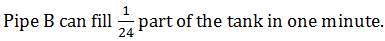
∴ Pipe B will fill the whole tank in 24 minutes.
Solution 2:
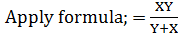
X= 12 minutes
Y=?
As per question;
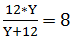
12Y= 8Y+96
4Y= 96
Y = 24 minutes
Question: 8 -
Two pipes working together can fill a fish tank in 12 minutes. If one pipe fills the fish tank 10 minutes faster than the second pipe, in what time the second pipe alone can fill the fish tank?
-
20
-
30
-
25
-
35
Answer:
30
Solution:
Let the first pipe fill the reservoir in X minutes
So, the second pipe will fill the reservoir in (X+10) minutes
As per question;
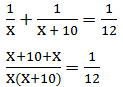
12X +120 + 12X = X2 + 10X
X2 +10X 24X -120 = 0
X2 14X -120 =0
X2 - 20X+6X 120=0
X(X-20) +6(X-20) =0
(X+6) (X-20) = 0
X = 20
∴Second pipe will fill the reservoir in 20 + 10= 30 minutes
Let the first pipe fill the reservoir in X minutes
So, the second pipe will fill the reservoir in (X+10) minutes
As per question;
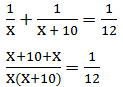
12X +120 + 12X = X2 + 10X
X2 +10X 24X -120 = 0
X2 14X -120 =0
X2 - 20X+6X 120=0
X(X-20) +6(X-20) =0
(X+6) (X-20) = 0
X = 20
∴Second pipe will fill the reservoir in 20 + 10= 30 minutes
Question: 9 -
20 buckets can fill a tank when the capacity of each bucket is 12 liters. If the capacity of each bucket is 10 liters, find the number of buckets required to fill the tank.
-
27 buckets
-
24 buckets
-
34 buckets
-
30 buckets
Answer:
24 buckets
Solution:
Capacity of each bucket = 12 liters
20 buckets can fill the tank. So, capacity of tank = 20 * 12= 240 liters
New capacity of bucket = 10 liters
So, 10 liters can be poured into the tank by one bucket
Capacity of each bucket = 12 liters
20 buckets can fill the tank. So, capacity of tank = 20 * 12= 240 liters
New capacity of bucket = 10 liters
So, 10 liters can be poured into the tank by one bucket
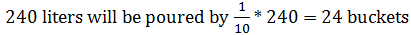
Question: 10 -
25 outlets working 6 hours a day, can empty a reservoir in 10 days. If only 15 outlets are operational and work for 4 hours a day, in how many days the reservoir can be emptied?
-
22 days
-
18 days
-
20 days
-
25 days
Answer:
25 days
Solution:
Apply formula used in work and time problems; M1D1T1W2 = M2D2T2W1
M1= 25 outlets, D1=10 days, T1= 6 hours/day, W2 = to fill the reservoir
M2= 15 outlets, D2=? T2 = 4 hours/day, W1= to fill the reservoir
W1=W2
So we have; M1D1T1= M2D2T2
25*10*6=15*D2*4
1500 = 60 * D2
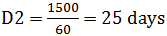
Apply formula used in work and time problems; M1D1T1W2 = M2D2T2W1
M1= 25 outlets, D1=10 days, T1= 6 hours/day, W2 = to fill the reservoir
M2= 15 outlets, D2=? T2 = 4 hours/day, W1= to fill the reservoir
W1=W2
So we have; M1D1T1= M2D2T2
25*10*6=15*D2*4
1500 = 60 * D2