Question: 11 -
A can fill a tank in 8 hours, B can fill the same in 12 hours, and C can fill the tank in 24 hours. If they are open at 2 am, 3 am, and 4am respectively, then at what time the tank will be completely fill?
-
7:20 am
-
6:00 am
-
6:40 am
-
5:00 am
Answer:
6:40 am
Solution:
At 2am: A starts and fill the tank in 8 hours.
At 3am: B starts and fill the tank in 12 hours.
At 4am: C starts and fill the tank in 24 hours.
Let the capacity of the tank = LCM of (A's, B's, and C's time)
Now, LCM of 8, 12, and 24 is 24.
i.e., the capacity of the tank = 24 litre
Now, A's one hour work = capacity of the tank/ time taken by A.
A's one hour work = 24/ 8 = 3litre/hour.
B's one hour work = 24/12 = 2litre/hour.
C's one hour work = 24/24 = 1litre/hour.
ATQ, between 2am to 3am, only A works = 3 unit
Between 3am to 4am, A and B works = 3+2 = 5 unit
Total work done till 4 am is 5+3 = 8 unit
Then the remaining work after 4am = 24-8 = 16unit
Now,
Between 4am to 5am, A, B, and C works = 3+2+1 = 6unit/hr
To complete the 16 unit work it requires 16/6 = 2[2/3], or 2:40min
That means the total work will complete at 4am+2hr+40min= 6:40 am
At 2am: A starts and fill the tank in 8 hours.
At 3am: B starts and fill the tank in 12 hours.
At 4am: C starts and fill the tank in 24 hours.
Let the capacity of the tank = LCM of (A's, B's, and C's time)
Now, LCM of 8, 12, and 24 is 24.
i.e., the capacity of the tank = 24 litre
Now, A's one hour work = capacity of the tank/ time taken by A.
A's one hour work = 24/ 8 = 3litre/hour.
B's one hour work = 24/12 = 2litre/hour.
C's one hour work = 24/24 = 1litre/hour.
ATQ, between 2am to 3am, only A works = 3 unit
Between 3am to 4am, A and B works = 3+2 = 5 unit
Total work done till 4 am is 5+3 = 8 unit
Then the remaining work after 4am = 24-8 = 16unit
Now,
Between 4am to 5am, A, B, and C works = 3+2+1 = 6unit/hr
To complete the 16 unit work it requires 16/6 = 2[2/3], or 2:40min
That means the total work will complete at 4am+2hr+40min= 6:40 am
Question: 12 -
A tank has two pipes. The first pipe can fill it in 45 minutes and the second can empty it in 1 hour. In what time will the empty tank be filled if the pipes be opened one at a time in alternate minutes?
-
2 hrs 55 min
-
4 hrs 48 min
-
3 hrs 40 min
-
5 hrs 53 min
Answer:
5 hrs 53 min
Solution:
Let pipe A can fill a tank in 45 minutes
Pipe B can empty in 1 hour = 60 minutes.
Now, take LCM of A and B to find the capacity of the tank
LCM of A (45) and B (60) = 180
That means assume the capacity of tank is 180 litres
Now, 1 minute work of A = 180/45 = 4 units
Now, 1 minute work of B = 180/60 = - 3 units
Here ?ve indicates empty tank per minute
But ATQ, the pipes are open alternatively, that means the net filling of tank in 2 minutes = 4-3 = 1 unit
Now, 176 units will be filled in 176*2 = 352 minutes.
Now, the remaining 4 litres will be filled in next 1 minute
i.e., 352 + 1 = 353 min = 60*5 = 300 + 53
Therefore, the time taken to fill the tank = 5 hrs + 53 min.
Let pipe A can fill a tank in 45 minutes
Pipe B can empty in 1 hour = 60 minutes.
Now, take LCM of A and B to find the capacity of the tank
LCM of A (45) and B (60) = 180
That means assume the capacity of tank is 180 litres
Now, 1 minute work of A = 180/45 = 4 units
Now, 1 minute work of B = 180/60 = - 3 units
Here ?ve indicates empty tank per minute
But ATQ, the pipes are open alternatively, that means the net filling of tank in 2 minutes = 4-3 = 1 unit
Now, 176 units will be filled in 176*2 = 352 minutes.
Now, the remaining 4 litres will be filled in next 1 minute
i.e., 352 + 1 = 353 min = 60*5 = 300 + 53
Therefore, the time taken to fill the tank = 5 hrs + 53 min.
Question: 13 -
Two pipes A and B individually can fill a tank in 15 hours, and 12 hours respectively, and C can empty the full tank in 4 hour. If all three pipes are open at 8, 9, and 11 am respectively. At what time tank will be completely empty?
-
1:35 pm
-
2:40 pm
-
1:00 pm
-
12:00 pm
Answer:
2:40 pm
Solution:
At 8am: A starts and fill the tank in 15 hours.
At 9am: B starts and fill the tank in 12 hours.
At 11am: C starts and empty the tank in 4 hours.
Let the capacity of the tank = LCM of (A's, B's, and C's time) Now, LCM of 15, 12, and 4 is 60.
i.e., the capacity of the tank = 60 litre
Now, A's one hour work = capacity of the tank/ time taken by A.
A's one hour work = 60/ 15 = 4litre/hour.
B's one hour work = 60/12 = 5litre/hour.
C's one hour work = 60/4 = 15litre/hour.
ATQ, between 8am to 9am, only A works = 4 units
Between 9am to 10am, A and B works = 4+5 = 9 units
Between 10am to 11am, A and B works = 4+5 = 9 units
Total work done till 11 am is 4+9+9 = 22 units
Now,
Between 11am to 12am, A, B, and C works = 4+5-15 = -6unit/hr
Here, -ve sign indicates C empty the tank.
That means after 11 am, every hour the tank will be empty by 6 units.
Now, we have to empty the 22 unit water that is stored till 11 am
So, the tank can be empty in 1 hour = 6 unit
Or, to empty 1unit water it requires 1/6 hour.
Or, 22 unit = (1/6) * 22 = 11/3
Or, 22 unit water can be empty in 3[2/3], or 3 hour + (2/3)*60 hour
Or, 3hour: 40min
That means the water that is stored till 11 am will be empty in 3hour: 40min
So, the time which requires to empty the tank is 11 hour+3 hour+40min = 2:40pm
At 8am: A starts and fill the tank in 15 hours.
At 9am: B starts and fill the tank in 12 hours.
At 11am: C starts and empty the tank in 4 hours.
Let the capacity of the tank = LCM of (A's, B's, and C's time) Now, LCM of 15, 12, and 4 is 60.
i.e., the capacity of the tank = 60 litre
Now, A's one hour work = capacity of the tank/ time taken by A.
A's one hour work = 60/ 15 = 4litre/hour.
B's one hour work = 60/12 = 5litre/hour.
C's one hour work = 60/4 = 15litre/hour.
ATQ, between 8am to 9am, only A works = 4 units
Between 9am to 10am, A and B works = 4+5 = 9 units
Between 10am to 11am, A and B works = 4+5 = 9 units
Total work done till 11 am is 4+9+9 = 22 units
Now,
Between 11am to 12am, A, B, and C works = 4+5-15 = -6unit/hr
Here, -ve sign indicates C empty the tank.
That means after 11 am, every hour the tank will be empty by 6 units.
Now, we have to empty the 22 unit water that is stored till 11 am
So, the tank can be empty in 1 hour = 6 unit
Or, to empty 1unit water it requires 1/6 hour.
Or, 22 unit = (1/6) * 22 = 11/3
Or, 22 unit water can be empty in 3[2/3], or 3 hour + (2/3)*60 hour
Or, 3hour: 40min
That means the water that is stored till 11 am will be empty in 3hour: 40min
So, the time which requires to empty the tank is 11 hour+3 hour+40min = 2:40pm
Question: 14 -
A cylindrical tank of diameter 25 cm is full of water. If 11 litres of water is drawn off, the water level in the tank will drop by
-
112/5
-
12
-
14
-
21/2
Answer:
112/5
Solution:
Volume of cylinder = π r2 h
π r2 h = 11 litres = 11000 cm3
Or 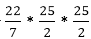 = 11000 cm3
= 11000 cm3
h = 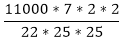
h = 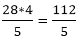 = 22
= 22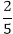 cm
cm
Volume of cylinder = π r2 h
π r2 h = 11 litres = 11000 cm3
Or 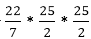 = 11000 cm3
= 11000 cm3
h = 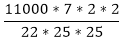
h = 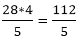 = 22
= 22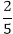 cm
cm