Question: 6 -
The radius of hemisphere is 3 cm. The ratio of its volume to the total surface area is
-
1: 1
-
2: 3
-
1: 3
-
2: 1
Answer:
2: 3
Solution:
Radius of hemisphere = 3 cm

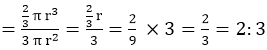
Ratio = 2: 3
Radius of hemisphere = 3 cm
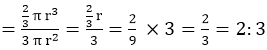
Ratio = 2: 3
Question: 7 -
If two spheres have their radii in the ratio 2: 3, the ratio of their volumes is
-
6 : 12
-
8 : 27
-
1 : 15
-
4 : 9
Answer:
8 : 27
Solution:
Let the radius of both the spheres be 'r' and 'R', respectively.
r: R = 2: 3
Volume of sphere = 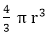
Ratio between the volume of spheres =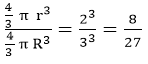
=8:27
Let the radius of both the spheres be 'r' and 'R', respectively.
r: R = 2: 3
Volume of sphere = 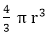
Ratio between the volume of spheres =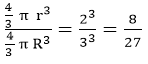
=8:27
Question: 8 -
Surface area of a sphere is 5544 cm2. Its volume will be
-
380808
-
30808
-
38808
-
380800
Answer:
38808
Solution:
Surface area of sphere = 4 π r2=5544 cm2
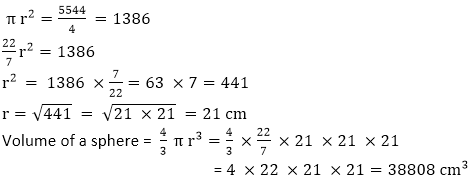
Volume of a sphere 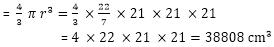
Surface area of sphere = 4 π r2=5544 cm2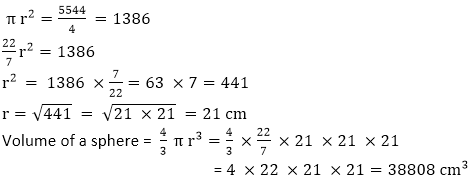
Volume of a sphere 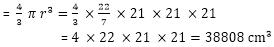
Question: 9 -
The radii of two cylinders are in the ratio of 2: 3 and their heights are in the ratio of 5: 3. The ratio of their volume is
-
20: 27
-
4: 9
-
20: 25
-
9: 4
Answer:
20: 27
Solution:
Let the radius of both cylinders be 2x and 3x.
Let the height of both cylinders be 5y and 3y.
Ratio of the volume of two cylinders 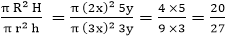
Ratio = 20: 27
Let the radius of both cylinders be 2x and 3x.
Let the height of both cylinders be 5y and 3y.
Ratio of the volume of two cylinders 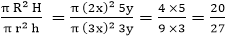
Ratio = 20: 27
Question: 10 -
If the curved surface area of a sphere is same as the curved surface area of a hemisphere, find the radius of the hemisphere.
-
2 times that of the sphere
-
sqrt(2) times that of the sphere
-
sqrt(3) times that of the sphere
-
Same as that of the sphere
Answer:
sqrt(2) times that of the sphere
Solution:
Curved surface area of a sphere = Curved surface area of a hemisphere
4 π R2= 2 π r2
2 R2= r2
Radius of hemisphere i.e. 'r' = 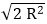 =
= 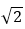 R
R
Curved surface area of a sphere = Curved surface area of a hemisphere
4 π R2= 2 π r2
2 R2= r2
Radius of hemisphere i.e. 'r' = 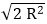 =
= 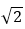 R
R