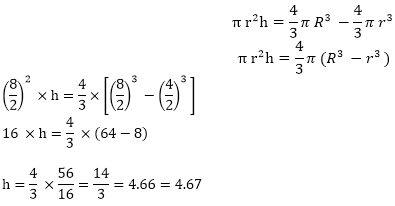Question: 11 -
The radius of road roller is 1 meter and length 7/22 meter. When it is rolled on a ground then it rolls 500 times to level the ground. But it was found that on 5% part of the ground, roller rolled twice. What is the total area of the ground?
-
950
-
975 sqrt(Π) m2
-
975
-
1000/Π2 m2
Answer:
950
Solution:
Let the area of the ground = x meter
The area covered in 1 revolution by the roller = 2Πrl
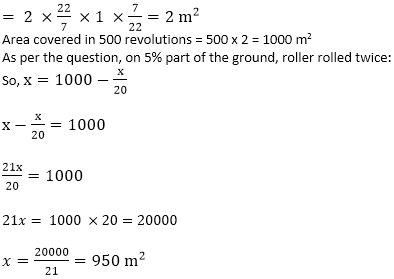
Let the area of the ground = x meter
The area covered in 1 revolution by the roller = 2Πrl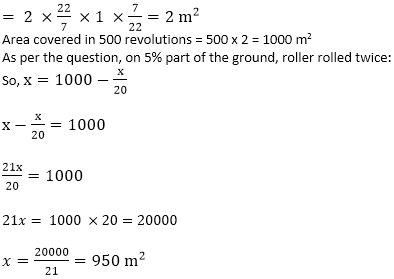
Question: 12 -
The length, breadth, and height of a brick are 10 cm, 4 cm, and 3 cm, respectively. Find the surface area of the brick?
-
160
-
164
-
154
-
156
Answer:
164
Solution:
Surface area of a Cuboid = 2(lb+ bh+ hl) cm2
So,
Surface area of a brick = 2(10*4+4*3+3*10) cm2
= 2(82) cm2= 164 cm2
Surface area of a Cuboid = 2(lb+ bh+ hl) cm2
So,
Surface area of a brick = 2(10*4+4*3+3*10) cm2
= 2(82) cm2= 164 cm2
Question: 13 -
A copper sphere of radius 3 cm is beaten and drawn into a wire of diameter 0.2 cm. The length of the wire is
-
21
-
36
-
18
-
9
Answer:
36
Solution:
Radius of wire =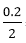 = 0.1
= 0.1
Volume of sphere = Volume of cylinder
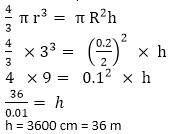
Radius of wire =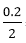 = 0.1
= 0.1
Volume of sphere = Volume of cylinder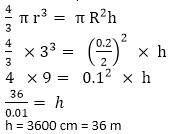
Question: 14 -
A 6 m long and 4 m wide cistern contains water up to a breadth of 1 m 25 cm. Find the total surface area of the surface immersed in water?
-
64
-
42
-
52
-
49
Answer:
49
Solution:
Area of the wet surface =
2[lb+ bh+ hl] - lb = 2 [bh+ lh] + lb
= 2[(4*1.25+6*1.25)] +6*4 = 49 m2
Solution 2:
The area of the wet surface= Area of the base + area of the two walls 2 * (4 *1.25) + area of the other two walls 2 * (6 * 1.25) cm
= 6*4 + 2 (4*1.25) + 2 (6*1.25)
= 24+ 10 + 15 = 49 m2
Area of the wet surface =
2[lb+ bh+ hl] - lb = 2 [bh+ lh] + lb
= 2[(4*1.25+6*1.25)] +6*4 = 49 m2
Solution 2:
The area of the wet surface= Area of the base + area of the two walls 2 * (4 *1.25) + area of the other two walls 2 * (6 * 1.25) cm
= 6*4 + 2 (4*1.25) + 2 (6*1.25)
= 24+ 10 + 15 = 49 m2
Question: 15 -
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted to form a solid cylinder of base diameter 8 cm. What is the height of the cylinder?
-
4.57
-
4.67
-
4.7
-
4.5
Answer:
4.67
Solution:
Let the height of the cylinder be h.
According to question:
Volume of cylinder = Volume of hollow sphere
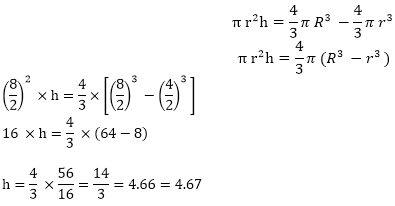
Let the height of the cylinder be h.
According to question:
Volume of cylinder = Volume of hollow sphere