Question: 31 -
A bird shooter was askgd how many birds he had in the bag. He replied that there were all sparrows but six, all pigeons but six, and all ducks but six. How many birds he had in the bag in all?
-
54
-
18
-
36
-
9
Answer:
9
Solution:
There were all sparrows but six' means that six birds were not sparrows but only pigeons and ducks.
Similarly, number of sparrows + number of ducks = 6 and number of sparrows + number of pigeons = 6.
This is possible when there are 3 sparrows, 3 pigeons and 3 ducks i.e. 9 birds in all.
There were all sparrows but six' means that six birds were not sparrows but only pigeons and ducks.
Similarly, number of sparrows + number of ducks = 6 and number of sparrows + number of pigeons = 6.
This is possible when there are 3 sparrows, 3 pigeons and 3 ducks i.e. 9 birds in all.
Question: 32 -
A is three times as old as B. C was twice-as old as A four years ago. In four years' time, A will be 31. What are the present ages of B and C ?
-
10, 46
-
9, 50
-
10, 50 -
9, 46
Answer:
9, 50
Solution:
We have : A = 3B ...(i) and
C - 4 = 2 (A - 4) ...(ii)
Also, A + 4 = 31 or A= 31-4 = 27.
Putting A = 27 in (i), we get: B = 9.
Putting A = 27 in (ii), we get C = 50.
We have : A = 3B ...(i) and
C - 4 = 2 (A - 4) ...(ii)
Also, A + 4 = 31 or A= 31-4 = 27.
Putting A = 27 in (i), we get: B = 9.
Putting A = 27 in (ii), we get C = 50.
Question: 33 -
Mr. Johnson was to earn £ 300 and a free holiday for seven weeks' work. He worked for only 4 weeks and earned £ 30 and a free holiday. What was the value of the holiday?
-
£ 330
-
£ 360
-
£ 300
-
£ 420
Answer:
£ 330
Solution:
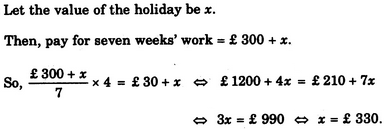
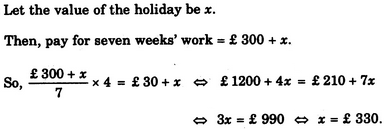
Question: 34 -
Today is Varun's birthday. One year, from today he will be twice as old as he was 12 years ago. How old is Varun today ?
-
25 years -
20 years
-
22 years
-
27 years
Answer:
| 25 years |
Solution:
Let Varan's age today = x years.
Then, Varan's age after 1 year = (x + 1) years.
Therefore x + 1 = 2 (x - 12)  x + 1 = 2x - 24
x + 1 = 2x - 24  x = 25.
x = 25.
Let Varan's age today = x years.
Then, Varan's age after 1 year = (x + 1) years.
Therefore x + 1 = 2 (x - 12)  x + 1 = 2x - 24
x + 1 = 2x - 24  x = 25.
x = 25.
Question: 35 -
What is the smallest number of ducks that could swim in this formation - two ducks in front of a duck, two ducks behind a duck and a duck between two ducks ?
-
3
-
7
-
9
-
5
Answer:
3
Solution:
Clearly, the smallest such number is 3.
Three ducks can be arranged as shown above to satisfy all the three given conditions.
Clearly, the smallest such number is 3.
Three ducks can be arranged as shown above to satisfy all the three given conditions.