Engineering Quantitative Aptitude English Reasoning General Knowledge Coding Others

Quiz: Arithmetic Reasoning

To View Tricks: Login Required

Number of Questions: 57

Question: 41 -

In a family, the father took 1/4 of the cake and he had 3 times as much as each of the other members had. The total number of family members is

Options:

  1. 3

  2. 12

  3. 7

  4. 10

    5. Answer:

    10
    Solution:

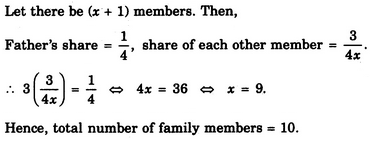
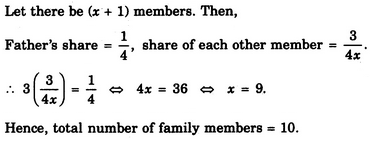
Question: 42 -

In a cricket match, five batsmen A, B, C, D and E scored an average of 36 runs. D Scored 5 more than E; E scored 8 fewer than A; B scored as many as D and E combined; and B and C scored 107 between them. How many runs did E score ?

Options:

  1. 20

  2. 28

  3. 62

  4. 45

    5. Answer:

    20
    Solution:

    Total runs scored = (36 x 5) = 180.

    Let the runs scored by E be x.

    Then, runs scored by D = x + 5; runs scored by A = x + 8;

    runs scored by B = x + x + 5 = 2x + 5;

    runs scored by C = (107 - B) = 107 - (2x + 5) = 102 - 2x.

    So, total runs = (x + 8) + (2x + 5) + (102 - 2x) + (x + 5) + x = 3x + 120.

    Therefore 3x + 120 =180  3X = 60  x = 20.

Question: 43 -

The number of boys in a class is three times the number of girls. Which one of the following numbers cannot represent the total number of children in the class ?

Options:

  1. 44

  2. 48

  3. 42

  4. 40

    5. Answer:

    42
    Solution:

    Let number of girls = x and number of boys = 3x.

    Then, 3x + x = 4x = total number of students.

    Thus, to find exact value of x, the total number of students must be divisible by 4.

Question: 44 -

A shepherd had 17 sheep. All but nine died. How many was he left with ?

Options:

  1. 8

  2. 17

  3. 9

  4. Nil

    5. Answer:

    9
    Solution:

    'All but nine died' means 'All except nine died' i.e. 9 sheep remained alive.

Question: 45 -

In three coloured boxes - Red, Green and Blue, 108 balls are placed. There are twice as many balls in the green and red boxes combined as there are in the blue box and twice as many in the blue box as there are in the red box. How many balls are there in the green box ?

Options:

  1. 36

  2. 45

  3. None of these

  4. 18

    5. Answer:

    None of these
    Solution:

    Let R, G and B represent the number of balls in red, green and blue boxes respectively.

    Then, .

    R + G + B = 108 ...(i),

    G + R = 2B ...(ii)

    B = 2R ...(iii)

    From (ii) and (iii), we have G + R = 2x 2R = 4R or G = 3R.

    Putting G = 3R and B = 2R in (i), we get:

    R + 3R + 2R = 108  6R = 108  R = 18.

    Therefore Number of balls in green box = G = 3R = (3 x 18) = 54.