Question: 16 -
The sides of a rectangular field are in the ratio 3: 4 and its area is 7500 m2. What is the cost of fencing it at 25 paise per meter?
-
Rs. 57.50
-
Rs. 67.50
-
Rs. 77.50
-
Rs. 87.50
Answer:
Rs. 87.50
Solution:
Ratio between the sides of rectangle = 3: 4
Let the ratio constant be x then,
Length = 3x and breadth = 4x
Area = L x B
7500=3x × 4x=12x2
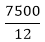 = x2=625
= x2=625
x=25
Length = 3 x 25 = 75 m, and Breadth = 4 x 25 = 100 m
Perimeter = 2(75 + 100) = 2 x 175 = 350 m
Cost of fencing 1 meter = 25 paise
Cost of fencing 350 m = 350 x 25 = 8750 paise
In rupees: Rs. 87.50
Ratio between the sides of rectangle = 3: 4
Let the ratio constant be x then,
Length = 3x and breadth = 4x
Area = L x B
7500=3x × 4x=12x2
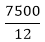 = x2=625
= x2=625
x=25
Length = 3 x 25 = 75 m, and Breadth = 4 x 25 = 100 m
Perimeter = 2(75 + 100) = 2 x 175 = 350 m
Cost of fencing 1 meter = 25 paise
Cost of fencing 350 m = 350 x 25 = 8750 paise
In rupees: Rs. 87.50
Question: 17 -
The sides of a rhombus are 10 cm in length, and one diagonal is 16 cm. The area of the rhombus is
-
93 cm2
-
96 cm2
-
95 cm2
-
94 cm2
Answer:
96 cm2
Solution:
When d1 and d2 are the diagonals of rhombus then,
The Side of rhombus = 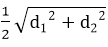
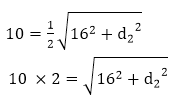
Squaring both sides
202 = 162 + d22
400 = 256 + d22
d22 = 400 - 256
d2 = √144
d2 = 12
Area of rhombus =1/2( d1 × d2 )
=1/2 ( 16 × 12 )=96 cm2
When d1 and d2 are the diagonals of rhombus then,
The Side of rhombus = 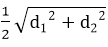
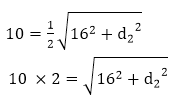
Squaring both sides
202 = 162 + d22
400 = 256 + d22
d22 = 400 - 256
d2 = √144
d2 = 12
Area of rhombus =1/2( d1 × d2 )
=1/2 ( 16 × 12 )=96 cm2
Question: 18 -
If the size of a tile is 9" by 9", how many tiles are required to cover a 12 ft. wide and 18 ft. long floor?
-
384
-
32
-
24
-
216
Answer:
384
Solution:
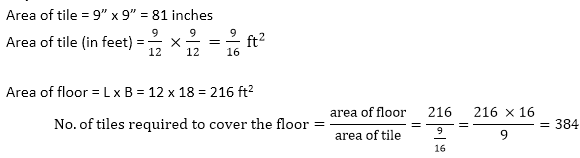
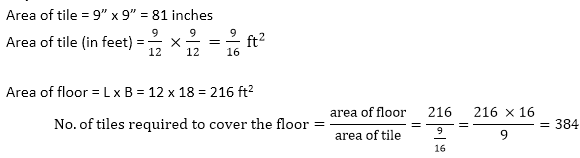
Question: 19 -
If each side of the square is increased by 50%, what will be the ratio between the new area and the original area of the square?
-
4: 9
-
4: 5
-
5: 4
-
9: 4
Answer:
9: 4
Solution:
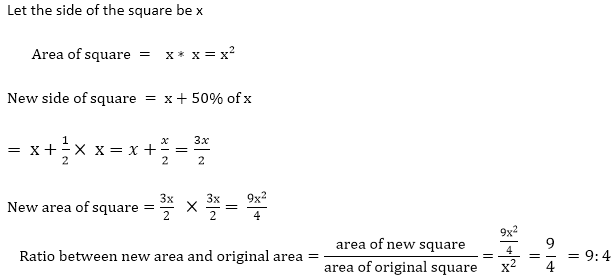
Question: 20 -
The difference between the length and the perimeter of a rectangle is 100 cms. What is the breadth of the rectangle?
-
80 cms
-
100 cms
-
Data Inadequate
-
60 cms
Answer:
Data Inadequate
Solution:
Let the length of the rectangle be 'x' and breadth of the rectangle be 'y'
According to the question:
2(x + y) - x = 100
2x + 2y - x = 100
x + 2y = 100
From this we cannot find 'y' (breadth), so the given data is inadequate.
Let the length of the rectangle be 'x' and breadth of the rectangle be 'y'
According to the question:
2(x + y) - x = 100
2x + 2y - x = 100
x + 2y = 100
From this we cannot find 'y' (breadth), so the given data is inadequate.